Hanbit the Developer
[Python] 백준 1504번: 특정한 최단 경로 본문
https://www.acmicpc.net/problem/1504
import sys
import heapq
input = sys.stdin.readline
def djikstra(start):
dp = {i: float('inf') for i in range(1, N + 1)}
dp[start] = 0
todo = [(start, 0)]
while todo:
curNode, curDist = heapq.heappop(todo)
if dp[curNode] < curDist:
continue
for b, c in graph[curNode]:
nextDist = curDist + c
if dp[b] > nextDist:
dp[b] = nextDist
heapq.heappush(todo, (b, nextDist))
return dp
if __name__ == '__main__':
N, E = map(int, input().split())
graph = {i: [] for i in range(1, N + 1)}
for _ in range(E):
a, b, c = map(int, input().split())
graph[a].append((b, c))
graph[b].append((a, c))
v1, v2 = map(int, input().split())
dp1 = djikstra(v1)
dp2 = djikstra(v2)
sum1 = dp1[1] + dp1[v2] + dp2[N]
sum2 = dp2[1] + dp2[v1] + dp1[N]
if sum1 == float('inf') and sum2 == float('inf'):
print(-1)
else:
print(min(sum1, sum2))
이 문제는 다익스트라를 통해 풀었다. 다익스트라는 특정 지점에서 다른 모든 노드까지의 최단거리를 알 수 있는 알고리즘이다.
우선 우리는 2개의 루트에 대한 최단거리를 알아내야한다.
1 -> v1 -> v2 -> N
1 -> v2 -> v1 -> N
아래의 사진을 보자.

여기서 1 -> v1의 루트를 대략 아래와 같다고 하자.

우리는 이것을 아래와 같이 단순히 표현할 것이다.

다시 돌아와서, 우리는 어떤 정보를 얻어야할까? 두 개의 루트에 대한 필요 정보는 아래와 같이 표현된다.


여기서 우리는 v1과 v2에서 시작하는 다익스트라를 총 2번 실행하면 모든 정보를 얻을 수 있다.
v1에 대해 수행하면 아래의 정보를 얻을 수 있다.
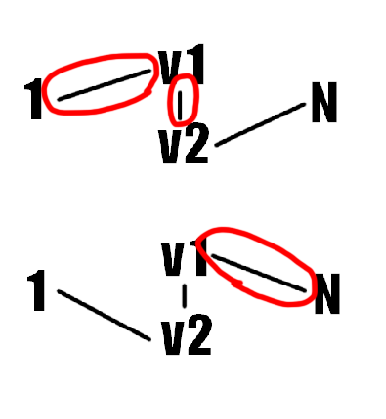
당연히 v2에 대해 수행하면 나머지 정보를 얻을 수 있게 된다. 다만 여기서 의문이 들 수도 있다. 다익스트라를 1에 대해 실행해서 1->v1, 1->v2를 얻어야하는 것이 아니냐는 의문 말이다. 하지만 이 그래프는 방향이 없는 그래프이므로 1->v1이나 v1->1이나 최단거리가 같다.
이렇게 하면 2개의 루트에 대한 합을 구할 수 있다.
sum1 = dp1[1] + dp1[v2] + dp2[N]
sum2 = dp2[1] + dp2[v1] + dp1[N]이 두 개의 합 중에 더 작은 것을 출력해주면 된다. 다만, 두 개가 모두 INF(도달할 수 없는 경우 값이 INF가 된다.)일 경우에는 -1을 출력해주면 된다.
'Algorithm > 백준' 카테고리의 다른 글
| [Python] 백준 2448번: 별 찍기 - 11 (0) | 2021.07.18 |
|---|---|
| [Python] 백준 1916번: 최소비용 구하기 (0) | 2021.07.16 |
| [Python] 백준 1305번: 광고 (0) | 2021.07.14 |
| [Python] 백준 1238번: 파티 (0) | 2021.07.13 |
| [Python] 백준 1043번: 거짓말 (0) | 2021.07.12 |



