HTD
[Python] Lazy Propagation (백준 10999번: 구간 합 구하기 2) 본문
https://www.acmicpc.net/problem/10999
10999번: 구간 합 구하기 2
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
Lazy Propagation을 통해, query, update 동작을 O(logN)으로 수행하여 이 문제를 해결한다. 이 글은 기본적인 Segment Tree를 알고 있다는 가정하에 설명한 것이다.
먼저, get_tree_length() 함수를 통해 적절한 길이를 얻고, 트리, lazy를 초기화 시킨다.
만약 N이 2의 제곱꼴이라면, 트리는 완전이진트리이므로 길이는 2*N-1이다.(인덱스가 1부터 시작하므로 -1을 제외하였다.)
그렇지 않을 경우에는, 길이가 2^(log(n)+1)-1가 된다. 여기서 log(n)+1은 트리의 높이이다.
세그먼트 트리를 위한 핵심 함수는 총 4개가 있다. 먼저 초기화 함수인데, 이것은 기존 세그먼트 트리의 것과 같다. 나머지는 update, query, propagate 함수가 있는데 모두 세그먼트 트리의 변형이 들어간다.
lazy propagation을 위해 예제 입력 1을 예시로 들어 설명한다.

초기 세그먼트 트리이다. 여기서 1 3 4 6, 즉 3~4번째 숫자에 6을 더하라는 update 동작을 수행하면 아래와 같이 된다.

2 2 5, 즉 2~5의 query를 수행하여도 위 상태 그대로이다. 아직까지는 lazy propagation의 영향이 없다.
다음으로 1 1 3 -2를 수행한 결과는 다음과 같다.

update 함수에서 if left <= start and end <= right에 해당하는 경우, 즉 현재의 start, end값이 update하려는 범위(left, right) 안에 들었을 때 수행하는 동작이 매우 중요하다. update 함수는 이 부분의 로직이 기본 세그먼트 함수의 update 함수와 다른 부분이다.
6의 값을 가진 노드의 하위 노드들은 모두 값이 바뀌지 않았다는 걸 알 수 있는데, 이것 때문에 lazy propagation(느린 전파)라는 이름이 붙게 된 것이다. 이 경우에는 현재 노드에 적절한 값(6)을 넣어주는데, (자식 노드의 갯수)*(더할 값)을 넣어줌으로써 곧바로 수행할 수 있다. 그리고 자식 노드들에 해당하는 lazy에 값을 넣어주고 바로 재귀함수를 끝낸다.
lazy에 값을 넣어줬다는 것은, 트리에 올바른 값을 넣어주는 작업을 나중으로 미루겠다고 선언한 것과 같다. 예시 입력 1에서 마지막으로 2 2 5를 수행해주는데 이에 대한 결과는 다음과 같다.
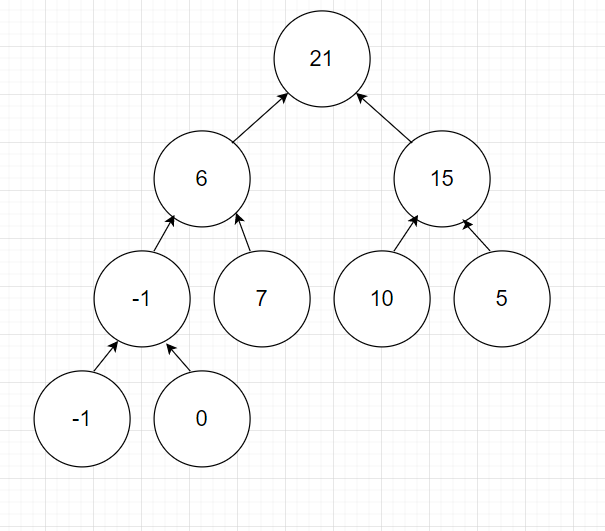
lazy 값이 사라졌으며, 트리가 적절한 값을 가졌음을 알 수 있다.
query 함수는 기존 세그먼트 트리의 것과 매우 흡사하지만, 앞에서 propagate 함수를 수행한다.
propagate 함수는, 앞서 update 함수에서 그렇게 하였듯이, 특정 노드에 lazy 값이 있으면, 그 노드에 올바른 값을 저장된 lazy를 통해 넣어주고, lazy값을 자식 노드에 전파해주는 역할을 한다. 즉, 쿼리를 진행하기에 앞서, propagete를 해주기 때문에 올바른 값을 얻을 수 있다는 것이다.
이쯤되면 직관적으로나마 감이 왔을 거라고 생각한다. 다음은 이에 대한 소스 코드이다.
import sys
import math
input = sys.stdin.readline
def get_tree_length():
if N & (N-1) == 0:
return 2*N
else:
return pow(2, math.ceil(math.log(N, 2)) + 1)
def initialize_segment_tree(index, start, end):
if start == end:
segment_tree[index] = nums[start]
return
mid = (start + end)//2
initialize_segment_tree(index*2, start, mid)
initialize_segment_tree(index*2+1, mid+1, end)
segment_tree[index] = segment_tree[index*2] + segment_tree[index*2+1]
def update_segment_tree(index, start, end, left, right, to_added):
propagate_segment_tree(index, start, end)
if right < start or end < left:
return
if left <= start and end <= right:
segment_tree[index] += (end - start + 1)*to_added
if start != end:
lazy[index*2] += to_added
lazy[index*2+1] += to_added
return
mid = (start + end)//2
update_segment_tree(index*2, start, mid, left, right, to_added)
update_segment_tree(index*2+1, mid+1, end, left, right, to_added)
segment_tree[index] = segment_tree[index*2] + segment_tree[index*2+1]
def query_segment_tree(index, start, end, left, right):
propagate_segment_tree(index, start, end)
if right < start or end < left:
return 0
if left <= start and end <= right:
return segment_tree[index]
mid = (start + end)//2
return query_segment_tree(index*2, start, mid, left, right) + query_segment_tree(index*2+1, mid+1, end, left, right)
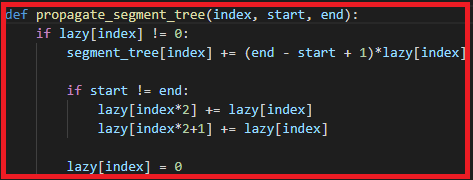
def propagate_segment_tree(index, start, end):
if lazy[index] != 0:
segment_tree[index] += (end - start + 1)*lazy[index]
if start != end:
lazy[index*2] += lazy[index]
lazy[index*2+1] += lazy[index]
lazy[index] = 0
if __name__ == '__main__':
N, M, K = map(int, input().split())
nums = [-1] + [int(input()) for _ in range(N)]
tree_length = get_tree_length()
segment_tree = [0]*tree_length
lazy = [0]*tree_length
initialize_segment_tree(1, 1, N)
for _ in range(M+K):
cur = list(map(int, input().split()))
if cur[0] == 1:
_, b, c, d = map(int, cur)
update_segment_tree(1, 1, N, b, c, d)
print(segment_tree)
print(lazy)
else:
_, b, c = map(int, cur)
print(query_segment_tree(1, 1, N, b, c))
print(segment_tree)
print(lazy)
아래 사진은 각 함수에서 lazy propagation을 위해 변형된 부분이다.


'Algorithm > 백준' 카테고리의 다른 글
| [Python] 백준 1395번: 스위치 (0) | 2021.09.03 |
|---|---|
| [Python] 백준 14725번: 개미굴 (0) | 2021.09.02 |
| [C] 백준 2750번: 수 정렬하기 (0) | 2021.08.31 |
| [Python] 백준 1256번: 사전 (0) | 2021.08.30 |
| [Python] 백준 1562번: 계단 수 (0) | 2021.08.29 |

