Hanbit the Developer
[탐색] Python - 2805번, 나무 자르기 본문
def getSmallerSumMeterIndex(sumMeter, m):
left, right = 0, len(sumMeter)-1
while left < right:
mid = (right + left)//2
if sumMeter[mid] < m:
right = mid
elif sumMeter[mid] > m:
left = mid + 1
elif sumMeter[mid] == m:
return mid
return left
N, M = map(int, input().split())
heights = list(map(int, input().split()))
heights.sort()
sumMeter = []
for i in range(N):
if i==0:
additionalCutHeight = heights[0]
prevSumMeter = sum(heights)
else:
additionalCutHeight = heights[i]-heights[i-1]
prevSumMeter = sumMeter[i-1]
sumMeter.append(prevSumMeter-additionalCutHeight*(N-i))
idx = getSmallerSumMeterIndex(sumMeter, M)
plus = N-idx
curMeter = sumMeter[idx]
curHeight = heights[idx]
if (M-curMeter)/plus == (M-curMeter)//plus:
print(curHeight-(M-curMeter)//plus)
else:
print(curHeight-(M-curMeter)//plus-1)1. 정렬
2. sumMeter 구하기... 각 나무의 높이에서 잘랐을 때 얻는 미터의 총합이라는 뜻입니다.
3. idx 구하기... 예시에서 M이 20이라고 했을 때, idx는 1입니다. 1의 위치에서 7의 나무를 얻었으니, 20을 얻을 때까지 1칸씩 '밑으로' 자르면 됩니다. 1칸을 잘랐을 때 (N-idx)씩 얻습니다. 즉, 4-1=3씩 얻게 되는데 이것의 의미는
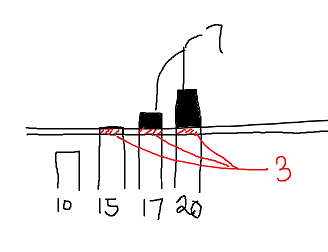
해당하는 나무들의 개수이죠. 그래서 N-idx입니다. 가령, M이 18~20이라는 이유로, idx가 3가 되었을 때는 1m씩 자를 때 잘리는 나무가 1개입니다.
다만, 1m씩 반복문으로 자르면서 잘라서 얻은 값을 계속 비교하는 것이 아니라, 한 줄의 연산으로 정답을 구할 수 있습니다. 결국 (idx의 높이)-(더 잘라야 하는 높이)가 답이 되는데,
여기서 (더 잘라야 하는 높이) = (더 얻어야 하는 나무 길이)/(자르면 얻는 나무의 길이)입니다.
다른 분들의 풀이를 보니, 높이를 이분탐색하는 경우가 많았습니다.
제 풀이는 NlogN + N + logN
높이를 이분 탐색한 경우에는 NlogM입니다.
'Algorithm > 백준' 카테고리의 다른 글
| [BackTracking] Python - 1987번, 알파벳 (0) | 2021.03.09 |
|---|---|
| [DP] Python - 1912번, 연속합 (0) | 2021.03.08 |
| [그리디] Python - 1946번, 신입 사원 (0) | 2021.03.03 |
| [문자열] Python - 2941번 크로아티아 알파벳 (0) | 2021.03.02 |
| [DP] Python - 11054번 가장 긴 바이토닉 부분 수열 (0) | 2021.02.26 |

