Hanbit the Developer
[C++] 백준 12784번: 인하니카 공화국 본문
https://www.acmicpc.net/problem/12784
12784번: 인하니카 공화국
인하니카 공화국은 1번~ N번까지 N개의 섬으로 이루어진 나라이다. 이 나라에서는 섬 간의 왕래가 매우 어려웠지만, 위대한 다리 설계자 ‘진’이 두 섬을 연결하는 다리를 최소한의 개수로 만들
www.acmicpc.net
> 접근
두 섬을 연결하는 다리를 최소한의 개수로 만들어 모든 섬 간의 왕래가 가능하도록 만들었다.
위 서술은 신장트리를 명시해주고 있다. 따라서 그래프를 탐색할 때 이전에 방문한 노드를 저장하고, 탐색 시 이전 노드를 블락해줌으로써 트리 탐색을 진행할 수 있다.
이제, 입력값을 트리라고 생각해보자.
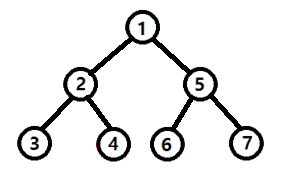
초기에 f(1)을 넣으면 결과값이 나오는 방향으로 재귀함수를 구성한다. f(1)에서 해야하는 것은, 아직까진 구체적으로 정해지진 않았으나, 결국 2, 5에 대해서 f를 수행한 뒤 그 합을 구해야할 것이다.
그럼, f(2), f(5)에서는 어떤 작업을 해야하는가? 선택지가 2개가 있다. 첫번째는 parent-node 간의 다이너마이트를 선택하는 것이며, 두번째는 childs의 다이너마이트를 모두 선택하는 것이다. 이 때 후자의 경우 현재 노드와 그 자식들의 다이너마이트를 선택하도록 하는 것이 아니라, 자식들에 대해 재귀함수를 돌려주는 것을 말한다.
추가로 같은 작업을 단순히 반복하므로, 트리의 인덱스에 상응하는 dp array를 만들어서, 결과값을 저장함으로써 시간복잡도를 줄일 수 있다.
#include <bits/stdc++.h>
#define INF 20001
using namespace std;
int N, M;
vector<pair<int, int>> graph[1001];
int dp[1001];
int f(int node, int parent) {
// DP가 초기값일 경우
if (dp[node] == 0) {
int res = INF;
// node-childs 간의 다이너마이트 선택
int sum = 0;
int i;
for (i = 0; i < graph[node].size(); i++) {
int child = graph[node].at(i).first;
int childWeight = graph[node].at(i).second;
if (child == parent) {
// parent-node 간의 다이너마이트 선택
res = childWeight;
continue;
}
if (graph[child].size() == 1) sum += childWeight;
else sum += f(child, node);
}
res = min(res, sum);
dp[node] = res;
}
return dp[node];
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int T;
cin >> T;
for (; T > 0;T--) {
cin >> N >> M;
// 초기화
int i;
for (i = 1; i < N + 1; i++) {
graph[i].clear();
dp[i] = 0;
}
// 입력
int a, b, c;
for (i = 0; i < M; i++) {
cin >> a >> b >> c;
graph[a].push_back({ b, c });
graph[b].push_back({ a, c });
}
// 출력
cout << f(1, 0) << "\n";
}
return 0;
}

'Algorithm > 백준' 카테고리의 다른 글
| [C++] 백준 6597번: 트리 복구 (1) | 2022.01.19 |
|---|---|
| [C++] 백준 2487번: 섞기 수열 (0) | 2022.01.14 |
| [C++] 백준 14942번: 개미(Sparse Table) (0) | 2022.01.07 |
| [C++] 백준 17612번: 쇼핑몰 (0) | 2022.01.06 |
| [C++] 백준 17069번: 파이프 옮기기 2 (0) | 2022.01.02 |




