HTD
CHT(Convex Hull Trick) 알고리즘 본문
정의
CHT는 특정 조건의 DP 점화식에 활용할 수 있는 최적화 기법입니다.
[조건]
1. dp[i] = min(a[j] * b[i] + dp[j]) (0 <= j < i)
2. 수열 a가 단조감소 한다.
dp[N]은 이중 포문을 돌아야 구할 수 있으므로 시간 복잡도는 O(N^2)입니다. 하지만 CHT를 활용하면 O(NlogN)으로 최적화를 할 수 있게 됩니다.
접근 방식
CHT에서는 dp[i]를 구할 때 '일차 함수'를 활용합니다. 아래 표에서 파란색 식을 보면 a[0] * b[i] + dp[0]의 꼴을 하고 있습니다. 여기서 b[i]를 x로 치환을 하면 a[0] * x + dp[0] 형태가 됩니다. 즉 j = 0일 때의 함수 f0는 a[0] * x + dp[0]입니다. j = 1일 때의 함수 f1은 a[1] * x + dp[1]입니다.
이 함수를 통해 dp[i]의 값을 구할 수 있습니다. 가령 dp[2]를 구할 때는 f0, f1에 b[2]를 x값으로 넣은 뒤 최소값을 구하면 됩니다.
일반화하면 dp[i]를 얻기 위해선 일차함수 f0, f1, ... fi-1에 x = b[i]를 넣은 뒤 최소값을 구해주면 됩니다.
| dp[i] | candidates |
| dp[0] | 0 (j = 0) |
| dp[1] | a[0] * b[1] + dp[0] (j = 0) |
| dp[2] | a[0] * b[2] + dp[0] (j = 0) |
| a[1] * b[2] + dp[1] (j = 1) | |
| dp[3] | a[0] * b[3] + dp[0] (j = 0) |
| a[1] * b[3] + dp[1] (j = 1) | |
| a[2] * b[3] + dp[2] (j = 2) |
스택: 함수 저장소
코드를 어떻게 구현해야 할지를 생각해보면 함수를 저장하는 공간이 필요해보입니다. CHT는 이 저장 공간으로 스택을 활용합니다. 코드는 대략 다음과 같습니다.
stack = deque() # Python에서 stack의 역할을 함
for i in range(1, N): # 1 <= i < N
fi = (a[i - 1], dp[i - 1]) # 일차함수 3x + 7를 (3, 7)로 표현할 수 있음
stack.append(fi) # 스택에 이번 함수 추가
x = b[i]
for 0 <= j < i: # 지금까지의 함수 싹 다 돌면서 x 대입해서 최소값 찾음
dp[i] = min(dp[i], stack[j].a * x + stack[j].b)함수 자르기
기존에는 dp[3]을 구할 때, 아래 사진처럼 f0, f1, f2에 x = b[3]를 넣어서 가장 작은 값인 초록색 함수에서의 값을 dp[3]로 취급하게 됩니다.

하지만 아래 사진과 같이 일차 함수의 아랫 부분만을 취급하게 된다면, 여러 값을 비교할 필요 없이 곧바로 최소값을 얻을 수 있습니다.

이를 어떻게 구현할지를 생각해봅시다. 위 사진을 보면, 각 함수가 만나는 교차점을 기준으로 최소값을 갖게 되는 함수가 변경됩니다. x = 0 ~ 8에서는 f0, x = 8~16에서는 f1, x = 16~에서는 f2가 항상 최소값을 갖게 됩니다. 따라서 교차점을 기준으로 함수를 자르면 됩니다.
f1 = 0.5x + 4일 때 이 함수를 [0.5, 4, 8]과 같이 표현할 수 있습니다. 0.5는 기울기, 4는 y절편, 8은 f1이 최소가 되는 시작점의 x 좌표입니다.
*교차점 구하는 법: (f2.b - f1.b) / (f1.a - f2.a)
이해를 위해 함수를 추가하는 과정을 순차적으로 설명하겠습니다.
[i = 1일 때]

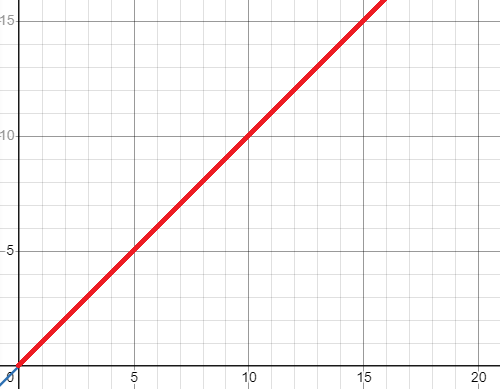
[i = 2일 때]
- 교차점 x 좌표가 8이므로 f1는 x = 8부터 시작한다.

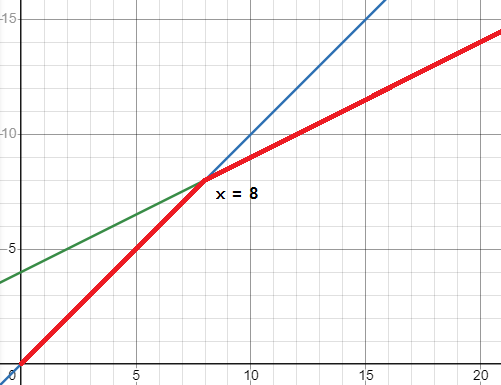
[i = 3일 때]
- 추가하고자 하는 함수 f2와 스택에서 가장 위에 있는(가장 최근에 추가한) 함수 f1과 교차점을 구한다.
- 교차점 x 좌표가 16이므로 f2는 x = 16부터 시작한다.

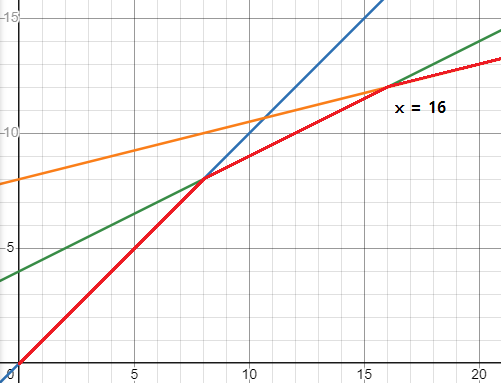
함수를 스택에 넣는 것을 코드로 구현하면 다음과 같습니다.
f_to_add = [a[i - 1], dp[i - 1], 0] # 함수 정의. start_x는 4번째 줄에서 수정할 예정
top_f = stack[top] # 가장 최근 함수 가져옴
intersection_x = get_intersection_x(f_to_add, top_f) # 교차점 구함
f_to_add[2] = intersection_x # 이번에 추가할 함수의 시작점(x)은 그 교차점의 x 좌표임
stack.append(f_to_add) # 스택에 넣음스택에서 최소값을 갖는 함수 찾기
이제 함수 여러 개가 스택에 있기 때문에 dp를 구하기만 하면 됩니다.
dp[3]을 구하고자 하는 상황에서 b[3] = 14라고 하면 이에 해당하는 최소 함수는 f1입니다. f1은 x = 8 ~ 16에서 최소값을 갖기 때문입니다.
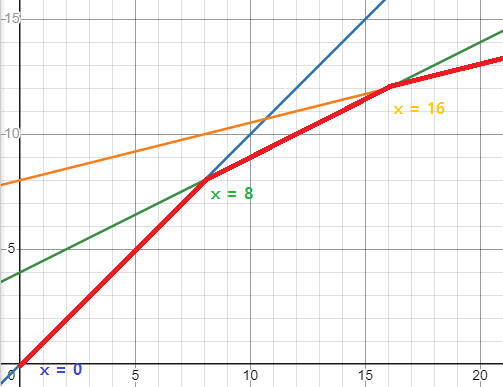
스택에서 최소값을 갖는 함수를 찾으려면, 스택에서 start_x를 기준으로 이진 탐색을 하면 됩니다. 즉, [0, 8, 16]에서 x = b[3] = 14로 이진탐색 해서 인덱스 1을 얻으면 됩니다.
코드는 다음과 같습니다.(파이썬에선 bisect_left를 해준 뒤 값을 1 빼주면 해당 인덱스를 더욱 편하게 구할 수 있습니다.)
x = b[i]
l, r = 0, len(stack) - 1
while l <= r:
m = (l + r) // 2
if stack[m].start_x >= x:
r = m - 1
else:
l = m + 1
stack_index = l - 1중간 정리(코드)
지금까지의 내용을 코드로 작성하면 다음과 같습니다. 생각보다 간단하다는 걸 알 수 있습니다.
A, B, START_X = 0, 1, 2
def get_intersection_x(f1, f2):
return (f2[B] - f1[B]) / (f1[A] - f2[A])
dp = [0] * n
stack = []
for i in range(1, N): # 1 <= i < N
f_to_add = [a[i - 1], dp[i - 1], 0] # dp[i] = min(a[j] * b[i] + dp[j])
# f_to_add의 시작점 구하기(교차점)
top_f = stack[top] # 가장 최근 함수 가져옴
intersection_x = get_intersection_x(f_to_add, top_f) # 교차점 구함
f_to_add[2] = intersection_x # 이번에 추가할 함수의 시작점(x)은 그 교차점의 x 좌표임
stack.append(f_to_add) # 스택에 넣음
# x에 맞는 함수 찾기(이진 탐색)
x = b[i]
l, r = 0, len(stack) - 1
while l <= r:
m = (l + r) // 2
if stack[m].start_x >= x:
r = m - 1
else:
l = m + 1
stack_index = l - 1
dp[i] = stack[stack_index][A] * x + stack[stack_index][B]스택에 함수를 추가할 때 발생하는 예외 처리
마지막으로 예외가 하나 있어서 이것만 처리해주면 구현이 끝입니다. 함수를 스택에 저장해주는 이유도 이 부분 때문입니다.
네 번째 함수 f3를 추가했는데 아래처럼 되었다고 가정하겠습니다. 이렇게 되면 f2가 의미가 없어지고 처리하기도 곤란해집니다. 만약 이대로 함수를 추가하게 되면, 각 함수들의 start_x는 [0, 8, 16, 13.6]가 됩니다.(13.6은 f3과 f2가 만나는 교차점 x) 정렬된 상태가 아니므로 이진탐색을 통한 최소 함수 찾기도 못하게 됩니다.

다음과 같은 과정을 통해 이 문제를 해결할 수 있습니다.
1. 추가할 함수(f3)와 스택 맨 위 함수(f2)의 교차점을 구한다.
2-1. 교차점이 스택 맨 위 함수(f2)의 start_x보다 앞에 있다면, 스택 맨 위 함수(f2)를 제거한다.(pop)
2-2. 정상적인 경우라면 반복문을 탈출한다.
3. 반복
아래 사진은 이 과정을 마친 후 스택의 모습입니다.

CHT 전체 코드
A, B, START_X = 0, 1, 2
def get_intersection_x(f1, f2):
return (f2[B] - f1[B]) / (f1[A] - f2[A])
dp = [0] * n
stack = []
for i in range(1, N): # 1 <= i < N
f_to_add = [a[i - 1], dp[i - 1], 0] # dp[i] = min(a[j] * b[i] + dp[j])
# stack에서 불필요한 함수 제거
while stack:
top_f = stack[top]
intersection_x = f_to_add.get_intersection_x(top_f)
if intersection_x < top_f.start_x: # 교차점이 top_f의 시작점보다 앞에 있음
stack.pop()
else: # 정상
f_to_add.start_x = intersection_x
stack.append(f_to_add)
break
# x에 맞는 함수 찾기(이진 탐색)
x = b[i]
l, r = 0, len(stack) - 1
while l <= r:
m = (l + r) // 2
if stack[m].start_x >= x:
r = m - 1
else:
l = m + 1
stack_index = l - 1
dp[i] = stack[stack_index][A] * x + stack[stack_index][B]
What's more?
1. 수열 a가 단조증가하고 최대값을 구하는 경우도 적용할 수 있다.
2. 수열 b가 단조증가한다면 이진탐색 없이 O(N)으로 풀 수 있다.
CHT 문제 풀어보기(백준)
https://www.acmicpc.net/problemset?sort=ac_desc&algo=89
'Algorithm' 카테고리의 다른 글
| [C++] 백준 1153번: 네 개의 소수 (0) | 2021.12.30 |
|---|---|
| [C] Prim-Jarnik Algorithm using Priorty Queue (0) | 2021.11.26 |
| [Python] 유클리드 호재법을 이용한 최소공배수와 최대공약수 (0) | 2021.10.04 |
